Answer:
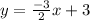
Explanation:
Step 1 - Calculate slope first via the equation:
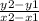
Where x1 and y1 are the coordinates of the first set whereas x2 and y2 are the second set. Plug the variables in:
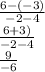
Which simplifies to:
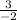
Now, in the line equation form we know x:
y = mx + c
y =
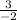 x + c
x + c
Step 2 - Calculate y intercept
Plug the variables of one point into the above equation:
y =
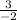 x + c
x + c
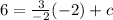

Meaning that the full line equation is:
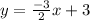
Hope this helps!