Question

Find the equation of the line

Answer 1

`y=-(1)/(3) + 5`

Explanation:

1. Pick two points (0,5) & (3,4)
2. find the slope
   `m= (y_(2) - y_1 )/(x_2 - x_1)` >>
   `m = (4-5)/(3-0) = -(1)/(3)`
3. Find y-intercept (where x is 0) >> y = 5

Answer 2

`\mathsf{y=-\frac13x+5}`

Explanation:

Slope-intercept form of a linear equation:
`\mathsf{y=mx+b}`

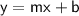
(where m is the slope and b is the y-intercept)

From inspection of the graph, the y-intercept is at (0, 5)

Therefore, b = 5

Choose another point on the line, e.g. (3, 4)

Now use the slope formula to find the slope:

`\mathsf{slope=(y_2-y_1)/(x_2-x_1)}`

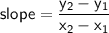
where:

• 
  `\mathsf{(x_1,y_1)=(0,5)}`
• 
  `\mathsf{(x_2,y_2)=(3,4)}`

`\implies \mathsf{slope=(5-4)/(0-3)=-\frac13}`

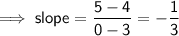
Therefore, the equation of the line is:

`\mathsf{y=-\frac13x+5}`