Question

What is the solution to the equation

x = –6
x = –1
x = 1
x = 2

Answer 1

A

Explanation:

EDGE 2019

Answer 2

Solving Equations

When we're solving equations, our prime goal is to isolate the variable. We can do this by using inverse operations to combine like terms.

Examples:

• The inverse operation of addition is subtraction, and vice versa.
• The inverse operation of an exponent is taking the root of the exponent, and vice versa.

Solving the Question

`\sqrt[3]{5x-4}=\sqrt[3]{7x+8}`

⇒ Here, both sides are being taken to the square root of 3. To remove this, we can raise both sides to the power of 3:

`(\sqrt[3]{5x-4})^3=(\sqrt[3]{7x+8})^3\\5x-4=7x+8`

⇒ Let's move our x variable to the right side of the equal sign and the numbers to the left side. Start by subtracting 5x from both sides:

`(\sqrt[3]{5x-4})^3-5x=(\sqrt[3]{7x+8})^3\\5x-4=7x+8-5x\\-4=2x+8`

⇒ Now, subtract 8 from both sides:

`-4-8=2x+8-8\\-12=2x`

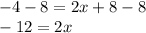
⇒ Finally, divide both sides by 2 to isolate x:

`(-12)/(2)=(2x)/(2)\\\\-6=x`

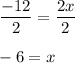
Answer

x = -6