The simplified form of
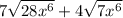 is
is
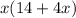 .
.
To simplify the expression
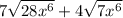 , you can first factor out any common factors from the radicands (the expressions inside the square roots).
, you can first factor out any common factors from the radicands (the expressions inside the square roots).
Step 1: Factor out common factors from the radicands.
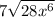 can be simplified as follows:
can be simplified as follows:
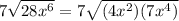
Similarly, for
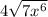 , you can factor out the common factors:
, you can factor out the common factors:
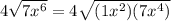
Step 2: Simplify the square roots of the factored expressions.
Now, let's simplify each square root individually:
For
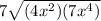 , you can split it into two square roots:
, you can split it into two square roots:
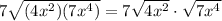
Simplify each square root separately:
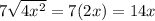
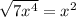
Similarly, for
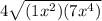 , you can split it into two square roots:
, you can split it into two square roots:
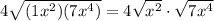
Simplify each square root separately:
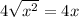
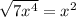
Step 3: Combine the simplified square roots.
Now that both square roots have been simplified, combine them back into a single expression:
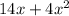
Step 4: Factor out the common factor, which is x:
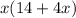
So, the answer is
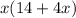 .
.