Question

Can someone solve this question ~


`\[ \lim_(x\to0) ( \sin(2x) + \sin(3x) )/(2x + \sin(3x) )`


`\large \boxed{ \mathfrak{Step\:\: By\:\:Step\:\:Explanation \;\; Required\: ~}}`
​

Answer 1

The limit of the given function as "x" approaches zero is 5/3

Limits of a function

Given the limit of a function expressed as:

• 
  `\lim_(x \to 0) (sin(2x)+sin(3x))/(2x+sin(3x))`

Applying l'hospital rule

Substitute the value of x into the function to have:

`\lim_(x \to 0) (sin(2x)+sin(3x))/(2x+sin(3x)) \\ =(sin(2(\infty))+sin(3(0)))/(2(0)+sin(3(0))) \\ =(0)/(0) (ind)`

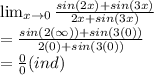
Apply the l'hospital rule by differentiating the function as shown:

`\lim_(x \to 0) (2cos(2x)+3cos(3x))/(2+3cos(3x)) \\=(2cos(2(0))+3cos3(0)))/(2(0)+3cos(3(0))) \\=(2+3)/(3)\\ =(5)/(3)`

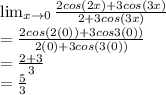
Hence the limit of the given function as "x" approaches zero is 5/3