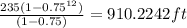Ok, so the question is based on geometric progression. Remember, the formula for calculating the nth-term of a geometric progression is:
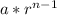 . The a in the expression stands for the 1st term of the sequence, and r is the common ratio of the elements of the sequence. Now let's take a look at the problem.
. The a in the expression stands for the 1st term of the sequence, and r is the common ratio of the elements of the sequence. Now let's take a look at the problem.
"A ping pong ball has a 75% rebound ration". We can infer that our common ratio, r, is 75% which is 0.75.
"When you drop it from a height of k feet...", this means the first height you drop it from, a.k.a, the first term.
Now going back to the expression, the nth-term =
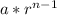 , we can substitute our common ration, 0.75 with r, and our 1st term, k, with a. This becomes:
, we can substitute our common ration, 0.75 with r, and our 1st term, k, with a. This becomes:
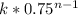 . This becomes our expression.
. This becomes our expression.
a. The highest height achieved by the ball after six bounces. Our nth-term here is 6, so let's use our expression to find the 6th term.
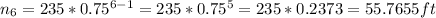
b. The total distance travelled by the ball when it strikes the ground for the 12th time. This involves the use of the sum of elements in the geometric progression. The formula for that is
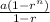 , provided that r is less than 1, which it is in this case, since 0.75 is less than one. Our nth-term here is 12, so we substitute.
, provided that r is less than 1, which it is in this case, since 0.75 is less than one. Our nth-term here is 12, so we substitute.