Answer:
x = 14
Explanation:
Given the following values for the rectangular vegetable garden:
x = length
(x - 4) = width
140 = area of the rectangular vegetable garden
To solve for the length of the garden, start by distributing x into the parenthesis:
x ( x - 4 ) = 140
x² - 4x = 140
Subtract 140 from both sides:
x² - 4x - 140 = 140 - 140
x² - 4x - 140 = 0
where a = 1, b = -4, and c = -140
Next, substitute the values for a, b, and c into the quadratic formula:
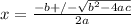

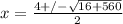

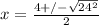
 ,
,
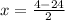
x = 14, x = -10
Given these two values for x, let's test each of them to see which value will provide a true statement:
x = 14
14( 14 - 4 ) = 140
14(10) = 140
140 = 140 (True statement).
x = -10
-10( -10 - 4 ) = 140
-10(-14) = 140
140 = 140 (True statement).
Even though both values for x provided a true statement, it wouldn't make sense to have a negative value for the length of a rectangular garden. Therefore, the correct answer is x = 14.