Answer:
y = -2x + 4
Explanation:
Perpendicular lines intersect at a point that form right angles; these lines also have negative reciprocal slopes, in which the product of their slopes result in a negative one (-1 ).
Given the linear equation in standard form, 3x - 6y = 7, and the point (3, -2):
Transform the standard form into slope-intercept form: y = mx + b
3x - 6y = 7
3x - 3x - 6y = -3x + 7
-6y = -3x + 7
Divide both sides by -6 to isolate y:
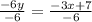
y = ½x - 7/6 (This is the slope-intercept form of the given equation, 3x - 6y = 7).
Now that we have the slope of the given equation,
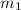 = ½, then we can determine that the slope of the other line must be
= ½, then we can determine that the slope of the other line must be
 = -2:
= -2:
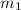 ×
×
 = ½ × -2 = -1
= ½ × -2 = -1
Next, using the slope of the other line,
 = -2, and the given point, (3, -2), substitute these values into the slope-intercept form to solve for the value of the y-intercept, b:
= -2, and the given point, (3, -2), substitute these values into the slope-intercept form to solve for the value of the y-intercept, b:
y = mx + b
-2 = -2(3) + b
-2 = -6 + b
Add 6 to both sides to isolate b:
-2 + 6 = -6 + 6 + b
4 = b (This is the y-intercept of the other line).
Therefore, the linear equation of the line that is perpendicular to 3x - 6y = 7 is:
y = -2x + 4