Answer:
The exact perimeter is
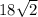 meters.
meters.
This is approximately 25.5 meters (nearest tenth).
The area of the rectangle is 36 square meters.
Explanation:
Area of a rectangle = width × length
Perimeter of a rectangle = (2 × width) + (2 × length)
Given:
- length =
 m
m - width =
 m
m
Perimeter



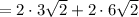
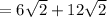
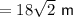
The exact perimeter is
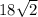 meters.
meters.
This is approximately 25.5 meters (nearest tenth).
Area

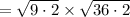

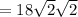
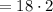
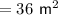
The area of the rectangle is 36 square meters.