Question

a block starts from rest and begins sliding down an incline. The block reaches a speed of 12 meters per second as it slides a distance of 50 meters. calculate the blocks rate of acceleration

Answer 1

Vf² = V₁² + 2ad

(12 m/s) ² = (0 m/s) ² + 2 (a) (50m)

a = 1.44 m/s ²

Answer 2

`\boxed {\boxed {\sf 1.44 \ m/s^2}}`

Step-by-step explanation:

We are asked to find the block's rate of acceleration.

We are given the final velocity, initial velocity, and distance. Therefore, we will use the following kinematic equation:

`{v_f}^2={v_i}^2+2ad`

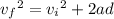
The block starts at rest or 0 meters per second. The block reaches a final velocity of 12 meters per second. The distance traveled is 50 meters.

• 
  `v_i`= 0 m/s
• 
  `v_f`= 12 m/s
• 
  `d`= 50 m

Substitute the values into the formula.

`(12 \ m/s)^2 = (0 m/s)^2 + 2a (50 \ m)`

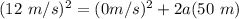
Solve the exponents.

• (12 m/s)² = 12 m/s * 12 m/s = 144 m²/s²
• (0 m/s)² = 0 m/s * 0 m/s = 0 m²/s²

`144 \ m^2/s^2= 0 m^2/s^2 + 2a (50 \ m)`

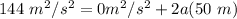
The 0 can be subtracted from both sides, or simply canceled.

`144 \ m^2/s^2 = 2a (50 \ m)`

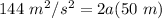
Multiply 2 and 50 meters.

`144 \ m^2/s^2 = (2 *50 \ m)* a`

`144 \ m^2/s^2 = (100 \ m)* a`

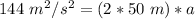
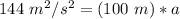
We are solving for a, so we must isolate the variable. It is being multiplied by 100 meters. The inverse of multiplication is division, so we divide both sides by 100 meters.

`\frac {144 \ m^2/s^2}{100 \ m}= ((100 \ m)*a)/(100 \ m)`

`\frac {144 \ m^2/s^2}{100 \ m}=a`

`1.44 \ m/s^2 =a`

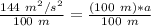
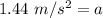
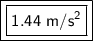
The block's rate of acceleration is 1.44 meters per second squared.