Answer: False. The number
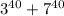 is not a multiple of 10
is not a multiple of 10
========================================================
Step-by-step explanation:
Let's look at a fairly small table of powers of 3 and 7. Check out the diagram below.
Notice that the units digits for each power involve the items from this set: {1,3,7,9}.
Furthermore, note that in each blue row we have the units digits add to 3+7 = 10 or 7+3 = 10. In order to be a multiple of 10, we need to have 0 as the units digit. Eg: 90 is a multiple of 0 for this reason.
So
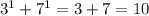 is one multiple of 10
is one multiple of 10
And so is
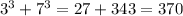
and so on. As the table shows, we have
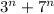 as some multiple of 10 as long as n is an odd positive integer. This contradicts the fact that 40 is an even integer for
as some multiple of 10 as long as n is an odd positive integer. This contradicts the fact that 40 is an even integer for
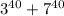 . So there's no way that this expression (whatever the massive number happens to be) is a multiple of 10. The units digit for this sum is not zero.
. So there's no way that this expression (whatever the massive number happens to be) is a multiple of 10. The units digit for this sum is not zero.
----------------------
You can use modular arithmetic as an alternative pathway to show that the given number isn't a multiple of 10
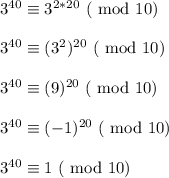
This shows that the units digit of
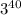 is 1
is 1
Also,
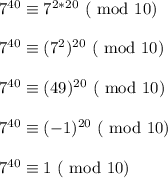
which looks very similar to the steps of
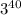 . This produces the same units digit. The two units digits add to 1+1 = 2, which is not zero and this is sufficient proof to show that
. This produces the same units digit. The two units digits add to 1+1 = 2, which is not zero and this is sufficient proof to show that
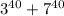 is not a multiple of 10.
is not a multiple of 10.
Going back to the table below, we see that the units digit of 1 show ups for both 3^n and 7^n whenever n is a multiple of 4. This applies to 40 because 40 = 4*10.