Answer:
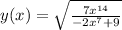
==========================================================
Step-by-step explanation:
The given differential equation (DE) is
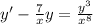
Which is the same as
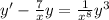
This 2nd DE is in the form
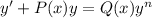
where
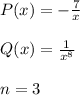
As the instructions state, we'll use the substitution
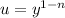
We specifically use
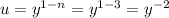
-----------------
After making the substitution, we'll end up with this form
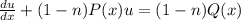
Plugging in the items mentioned, we get:
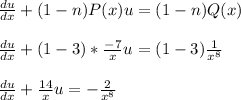
We can see that we have a new P(x) and Q(x)
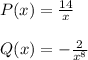
-------------------
To solve the linear DE
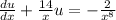 , we'll need the integrating factor which I'll call m
, we'll need the integrating factor which I'll call m
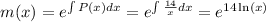
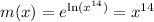
We will multiply both sides of the linear DE by this m(x) integrating factor to help with further integration down the road.
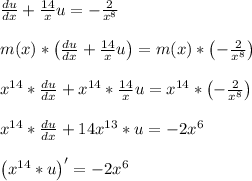
It might help to think of the product rule being done in reverse.
Now we can integrate both sides to solve for u
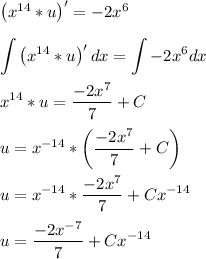
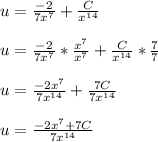
Unfortunately, this isn't the last step. We still need to find y.
Recall that we found
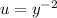
So,
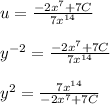
We're told that y(1) = 1. This means plugging x = 1 leads to the output y = 1. So the RHS of the last equation should lead to 1. We'll plug x = 1 into that RHS, set the result equal to 1 and solve for C
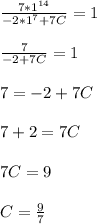
So,
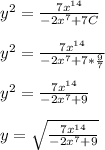
We go with the positive version of the root because y(1) is positive, which must mean y(x) is positive for all x in the domain.