Let's say we wanted to check if 16 was a perfect square or not.
What we do is subtract off the list of odd numbers {1,3,5,7,9,...}. If we reach 0 at any point, then the step number is what the square root will be.
So we'll start with 16 and subtract off 1 to get 15. Then from 15, we subtract off 3 to get 12. From 12, we subtract off 5 to get 7. This process is laid out below
- 16-1 = 15
- 15-3 = 12
- 12-5 = 7
- 7-7 = 0
By step 4, we reach 0. This indicates that
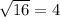
Note: The numbers to the left of the decimal point indicate the step number. All values mentioned are whole numbers.
-------------------
Here's another example. I'll start with 49
- 49 - 1 = 48
- 48 - 3 = 45
- 45 - 5 = 40
- 40 - 7 = 33
- 33 - 9 = 24
- 24 - 11 = 13
- 13 - 13 = 0
We reach 0 at step 7, therefore
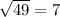
-------------------
If we started with some non-perfect square, say 50, then we'd get this:
- 50 - 1 = 49
- 49 - 3 = 46
- 46 - 5 = 41
- 41 - 7 = 34
- 34 - 9 = 25
- 25 - 11 = 14
- 14 - 13 = 1
- 1 - 15 = -14
As you can see, we don't reach 0, which means 50 is not a perfect square. The closest we get is 1 and that happens on the 7th step. This suggests
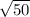 is closest to 7. It turns out that
is closest to 7. It turns out that
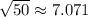 which helps confirm that previous statement.
which helps confirm that previous statement.