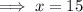Answer:
Question (a)
Given equation:
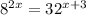
8 can be written as
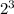
32 can be written as
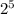
Therefore, we can rewrite the equation with base 2:
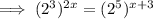
------------------------------------------------------------------------------
Question (b)
To solve:
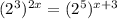
Apply the exponent rule
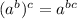 :
:
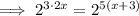
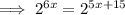
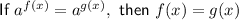 :
:
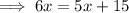
Subtract
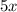 from both sides:
from both sides: