Question

How to solve I can’t do it

Answer 1

10.94

Explanation:

The standard deviation is calculated by using the following formula:

`s=\sqrt{(1)/(N-1)sum(xi -x)^2}`

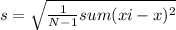
This means that N is the total number of cases you want to take into account, times the sum of x at the ith position - x squared.

In other words, the standard deviation in your example implies the following:

26 is the first value, so i = 1, 34 is the second value, so i = 2, 18 where i = 3, and so on and so forth, until you reach the end, which is 6 (so the initial value is 1 and the last one is 6).

You're doing a sum over an iteration of all the numbers in your sample.

So applying the sum of all of the numbers, it gives us the following:

`(26-28)^2+(34 - 28)^2+(18 - 28)^2 ... (41 - 28)^2`

`= (598)/(5) \\=119.6\\`

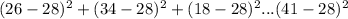
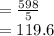
The sum of all of the numbers in your sample is equal to 119.6.

Substitute into the equation once again:

`s=√(119.6)`

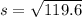
Where the square root of 119.6 is 10.93617...

Rounded to two decimal places: 10.94