Question

Help me plsss.... I need it tomorrow ​

Answer 1

see explanation

Explanation:

To find a , substitute the coordinates of the point on the curve into the equation, that is

(1)

y = ax² (3, 18)

18 = a × 3² = 9a ( divide both sides by 9 )

2 = a , then

y = 2x² is the equation

(2)

y = ax² (- 2, 30 )

30 = a × (- 2)² = 4a ( divide both sides by 4 )

7.5 = a , then

y = 7.5x² is the equation

(3)

y = ax² (4, 8 )

8 = a × 4² = 16a ( divide both sides by 16 )

`(8)/(16)` =
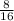`(1)/(2)` = a , then

y =
`(1)/(2)` x² is the equation

(4)

y = ax² (- 1, - 2 )

- 2 = a × (- 1)² = a , then

y = - 2x² is the equation

(5)

y = ax² (2, - 12 )

- 12 = a × 2² = 4a ( divide both sides by 4 )

- 3 = a , then

y = - 3x² is the equation

(6)

y = ax² (- 3, - 3 )

- 3 = a × (- 3)² = 9a ( divide both sides by 9 )

`(-3)/(9)` = -
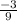`(1)/(3)` = a , then

y = -
`(1)/(3)` x² is the equation