Answer:
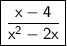
Explanation:
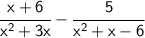
Factor x² + 3x, and x²+ x - 6
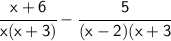
To add or subtract expressions, we expand them to make their denominators the same, LCM of x(x+3) and (x-2)(x+3) is x(x-2) (x+3).
Multiply
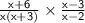 and
and


Here,
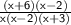 and
and
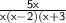 have the same denominators, we will subtract them by subtracting their numerators:
have the same denominators, we will subtract them by subtracting their numerators:

*Multiply (x+6)(x-2)-5x:
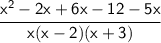
Combine like terms: x² - 2x + 6x - 12 - 5x
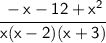
Now, factor expressions that are not already factored:
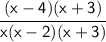
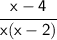
Expand:
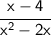
__________________________