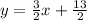Answer:
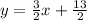
Explanation:
Perpendicular lines have negative reciprocals slopes, in which the product of their slopes result in -1.
Since the slope of the given line is m1 = -2/3, its negative reciprocal must be m2 = 3/2:
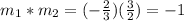
Next, we'll use the slope of the other line, m = 3/2, and the given point, (-3, 2) to solve for the y-intercept of the other line by substituting the values into the slope-intercept form:
y = mx + b
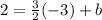
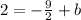
Add 9/2 to both sides to isolate b:
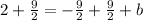
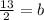
Therefore, the equation of the line perpendicular to
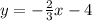 is:
is: