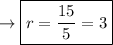Answer:
r = 3
Explanation:
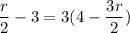
The first step to solve for "r" is to simplify the distributive property on the RHS. To simplify the distributive property, we need to multiply the term outside the parenthesis with the terms inside the parenthesis.
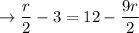
Now, add 9r/2 and 3 both sides to isolate the constants and variables.
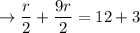
Simplify both sides.
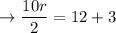
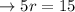
Divide 5 both sides.