Question

Solve each system of linear equations using the elimination mehod

-8x + 10y = -22
8x - 15y = 17

Answer 1

solution: x = 4, y = 1 or (4, 1)

Explanation:

To solve the system of linear equations using the elimination method, simply add both equations together (since the coefficeints of x have opposite signs):

-8x + 10y = -22

+ 8x - 15y = 17

- 5y = -5

Divide both sides by -5 to solve for y:

`(-5y)/(-5) = (-5)/(-5)`

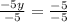
y = 1

Next, substitute the value of y into one of the equations to solve for x:

-8x + 10y = -22

-8x + 10(1) = -22

-8x + 10 = -22

Subtract 10 from both sides

-8x + 10 - 10 = -22 - 10

-8x = -32

Divide both sides by -8 to solve for x:

`(-8x)/(-8) = (-32)/(-8)`

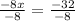
x = 4

Therefore, the solutions to the given systems of linear equations are: x = 4, y = 1 or (4, 1).

Answer 2

Answer: y = 1 and x = 4

Explanation:

-8x + 10y = -22

8x - 15y = 17

-----------------------

- 5y = -5 Add the two equations to eliminate x

y = 1 Solve for y

=====

8x - 15y = 17 (y = 1) Use y=1 in either equation

8x - 15 = 17

8x = 32

x = 4 Ta da