Question

A high jumper reaches a height of 2.1 m. If they have a mass of 65 kg, what is the gravitational potential energy at the highest point in the jump?

Answer 1

`\boxed {\boxed {\sf 1337.7 \ Joules}}`

Step-by-step explanation:

We are asked to find the gravitational potential energy at the highest point in the jump.

Gravitational potential energy is the energy an object possesses due to its position in a gravitational field. It is calculated using the following formula:

`GPE= m * g * h`

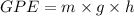
The mass of the jumper is 65 kilograms and they reach a height of 2.1 meters. Assuming this situation is occurring on Earth, the acceleration due to gravity is 9.8 meters per second squared.

• m= 65 kg
• g= 9.8 m/s²
• h= 2.1 m

Substitute the values into the formula.

`GPE = 65 \ kg * 9.8 \ m/s^2 * 2.1 \ m`

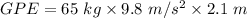
Multiply the numbers together.

`GPE=637 kg*m^2/s^2 * 2.1 \ m`

`GPE=1337.7 \ kg*m^2/s^2`

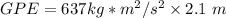
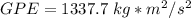
Convert the units. 1 kilogram meter squared per second squared is equal to 1 Joule, so our answer of 1337.7 kg*m²/s² is equal to 1337.7 J.

`GPE= 1337.7 \ J`

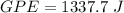
The gravitational potential energy at the highest point in the jump is 1337.7 Joules.