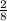Answer:
The slope is
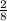
Explanation:
Take the general equation of a straight line
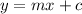
Here
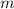 is the slope of the line.
is the slope of the line.
So let's get the equation of the line in the question in the same form.
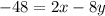
Add
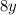 to both sides:
to both sides:
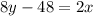
Add
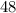 to both sides:
to both sides:
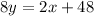
Divide by
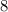 to get it into the general equation:
to get it into the general equation:
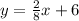
Now compare it to the general equation to find the value of
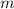 . The value of
. The value of
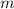 is the coefficient of
is the coefficient of
 which we can see is
which we can see is