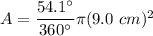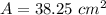Question

Circle A has a radius of 9.0 cm. The shortest distance between B and C on the circle is 8.5 cm. What is the approximate area of the shaded portion of circle A?

30.0 cm²

38.25 cm²

56.5 cm²

254.5 cm²

Answer 1

38.25 cm²

Explanation:

We use the formula for the length of an arc to find the central angle of the sector of the circle.

Then we use the formula for the area of a sector of a circle to find the area.

Length of arc of circle of radius r:

`s = (n)/(360^\circ)2 \pi r`

s = arc length

n = measure of the central angle of the sector

`s = (n)/(360^\circ)2 \pi r`

`8.5~cm = (n)/(360^\circ)2 \pi * 9.0~cm`

`n = 54.1^\circ`

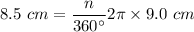
Area of sector of circle of radius r:

`A = (n)/(360^\circ) \pi r^2`

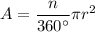
A = area of sector of circle

n = measure of the central angle of the sector

`A = (54.1^\circ)/(360^\circ) \pi (9.0~cm)^2`

`A= 38.25~cm^2`