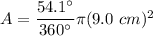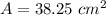Answer:
38.25 cm²
Explanation:
We use the formula for the length of an arc to find the central angle of the sector of the circle.
Then we use the formula for the area of a sector of a circle to find the area.
Length of arc of circle of radius r:
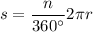
s = arc length
n = measure of the central angle of the sector
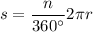
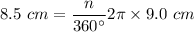
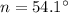
Area of sector of circle of radius r:
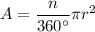
A = area of sector of circle
n = measure of the central angle of the sector