Question

Solving systems of equations by substitution 2x - 3y = 19
x - 2y = 11​

Answer 1

`\boxed {\boxed {\sf (5, -3)}}`

Explanation:

We are asked to solve the system of equations by substitution. We must isolate a variable and plug it into the other equation.

We are given these 2 equations;

`2x-3y=19`

`x-2y=11`

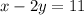
1. Isolate a Variable

We can easily isolate x in the 2nd equation. 2y is being subtracted from x. The inverse operation of subtraction is addition. Add 2y to both sides of the equation.

`x-2y+2y=11 +2y \\x= 11+2y`

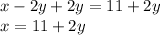
2. Substitute and Solve for y

x is equal to 11 + 2y, so we can substitute this expression in for x in the 1st equation.

`2x-3y=19`

`2(11+2y)-3y=19`

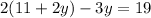
Now we can solve for y by isolating the variable First, distribute the 2. Multiply each term in parentheses by 2.

`(2*11) + (2*2y) -3y = 19`

`22 + 4y-3y = 19`

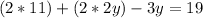
Combine the like terms.

`22+y=19`

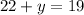
22 is being added to y. The inverse operation of addition is subtraction. Subtract 22 from both sides of the equation.

`22-22+y=19-22\\y= 19-22 \\y= -3`

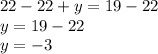
3. Solve for x

We know that y is equal to -3, so we can plug it back into either original equation and solve for x. Let's use the 2nd equation.

`x-2y=11`

`x-2(-3)=11`

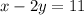
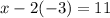
Multiply -2 and -3.

`x+6=11`

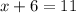
6 is being added to x. The inverse operation of addition is subtraction. Subtract 6 from both sides of the equation.

`x+6-6=11-6\\x=11-6 \\x=5`

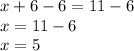
We found that y=-3 and x=5. Coordinate points are written as (x,y), so the solution for this system of equations is (5, -3).