Question

Use the polygon tool to draw a right triangle with hypotenuse AB?​

Answer 1

The coordinates of point C are therefore (-3, 2).

To draw a right triangle with hypotenuse AB, we need to find the coordinates of points A and B and then determine a third point C such that triangle ABC is a right triangle with AB as the hypotenuse.

we can estimate the coordinates of points A and B:

- Point A appears to be at approximately (-3, -1)

- Point B appears to be at approximately (0, 2)

We can follow these steps to draw the right triangle:

1. Determine the Length of AB:

Use the distance formula to find the length of AB.

`\( AB = √((x_2 - x_1)^2 + (y_2 - y_1)^2) \)`

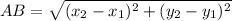
where
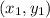`\( (x_1, y_1) \)` are the coordinates of point A and
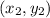`\( (x_2, y_2) \)` are the coordinates of point B.

2. Choose a Third Point C:

Point C must be on either the x-axis or the y-axis to ensure a right angle at C. We can select C such that it is vertical above or below A or horizontal to the left or right of B.

3. Calculate the Coordinates of C:

If C is vertical above or below A, its x-coordinate will be the same as A's, and its y-coordinate will be determined by the length of segment AC or BC.

If C is horizontal to the left or right of B, its y-coordinate will be the same as B's, and its x-coordinate will be determined by the length of segment AC or BC.

4. Use the Polygon Tool:

Once we have the coordinates of all three points, we can use the polygon tool to connect these points to form the right triangle.

Let's calculate the precise coordinates of C and the lengths of AC and BC using Python.

The length of the hypotenuse AB is
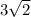`\(3√(2)\)` units. Since we are considering point C to be vertically above A, the horizontal distance BC is 3 units (the same as the distance from A to B on the x-axis), and the y-coordinate of point C is 2 units. Thus, point C has the same x-coordinate as A, which is -3, and a y-coordinate of 2.

With these coordinates, you can now use the polygon tool to draw the triangle:

1. Start at point A (-3, -1).

2. Draw a line from A to B (0, 2).

3. From B, draw a vertical line straight down to meet the x-axis at the same x-coordinate as A, which will be point C (-3, 2).

4. Draw a line from C back to A to complete the triangle.

This will give you a right triangle ABC with AB as the hypotenuse. The length of AC, the vertical side, is
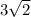`\(3√(2)\)` units (the same as AB), and the length of BC, the base, is 3 units.

Answer 2

in the -1,-1

Explanation: