Answer:
The parallel equation is y=
 x-5.
x-5.
The perpendicular equation is y=
 x-5.
x-5.
Explanation:
First solve for y.
-5x+2y=8
2y=5x+8
y=
 x+4
x+4
A line is parallel if it has the same slope, but different y-intercepts.
The y-intercept of the given point is -5, so the new slope will be y=
 x-5
x-5
To find a perpendicular line, you find the negative reciprocal of the given slope.
So you find
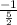 , which is equal to
, which is equal to
 .
.
The perpendicular equation is y=
 x-5.
x-5.