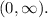f(x) is increasing on the intervals (-4, -3), (-2, -1),
 , and the intervals where f'(x) > 0 on the x-axis.
, and the intervals where f'(x) > 0 on the x-axis.
To determine the intervals on which the function y = f(x) is increasing, we can analyze the graph of f'(x), which represents the derivative of f(x).
From the given graph of f'(x):
1. It starts between 0 and 1 on the x-axis and 4 on the y-axis.
2. Passes through the point (1, 2).
3. Increases to between 3 and 4 on the x-axis and 3 on the y-axis.
The intervals on which f(x) is increasing correspond to the intervals where f'(x) > 0, as the derivative indicates the rate of change.
Based on the given information:
1. f'(x) > 0 between 0 and 1 on the x-axis.
2. f'(x) > 0 between 3 and 4 on the x-axis.
These intervals suggest that f(x) is increasing on the corresponding intervals.
Now, let's consider the inverted U-shaped curve for f(x) with the given points (-4, -2), (-3, 0), (-2, -1), (-1, 0), and (0, -2). Between these points, the function f(x) is increasing.
Therefore, the intervals on which f(x) is increasing are (-4, -3), (-2, -1), and