Question

I need an answer ASAP​

Answer 1

(B) 3

Explanation:

Qualitative answer. As x grows larger and larger, the contribute of lower degree terms (and constants) becomes irrelevant, and you rewrite everything picking the highest term for both numerator and denominator

`\lim\limits_(x \to \infty) (√(9x^4))/(x^2) $\lim\limits_(x \to \infty) (3x^2)/(x^2)=3`

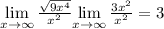
Analitically.

Collect
`9x^4` in the numerator under the square root,
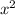`x^2` in the denominator.

`\lim\limits_(x \to \infty) \frac{\sqrt{9x^4(1+(1)/(9x^4))}}{x^2(1-(3)/(x)+(5)/(x^2))} = \lim\limits_(x \to \infty)\frac{3x^2\sqrt{(1+(1)/(9x^4))}}{{x^2(1-(3)/(x)+(5)/(x^2))}} = 3`

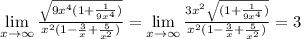
At this point the way you deal with it is the usual. Anything inside the bracket goes to 0 besides the lead coefficients (1 in both cases) and you're left with 3.