Question

The polynomial of degree 5, P(2), has leading coefficient 1, has roots of multiplicity 2 at x = 4 and

x = 0, and a root of multiplicity 1 at 3 3.
Find a possible formula for P(x).
P(x)

Answer 1

`P(x)=x^(5) +x^(4) -5x^(3) +3x^(2)`

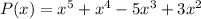
Explanation:

Each root corresponds to a linear factor, so we can write:

`P(x)=x^(2) (x-1)^(2) (x+3)\\=x^(2) (x^(2) -2x+1(x+3)\\\\=x^(5) +x^(4) -5x^(3) +3x^(2)`

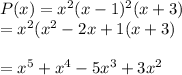
Any polynomial with these zeros and at least these multiplicities will be a multiple (scalar or polynomial) of this
`P(x)`

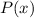
Footnote

Strictly speaking, a value of
`x` that results in
`P(x)=0` is called a root of

`P(x)=0` or a zero of
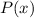`P(x)` . So the question should really have spoken about the zeros of
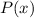`P(x)` or about the roots of
`P(x)=0`