We'll need the slope formula which is
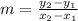
We subtract the y values together, and divide that over the difference in the x values when subtracted in the same order.
Let's find the slope of line DE
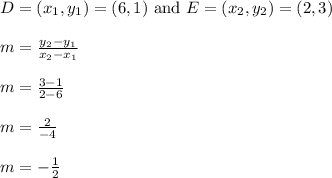
The slope of line DE is -1/2.
Next, compute the slope of line EF
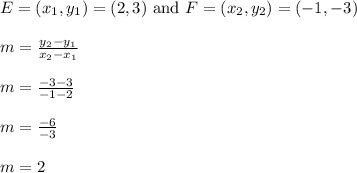
The slope of line EF is 2.
Lastly, compute the slope of line FD
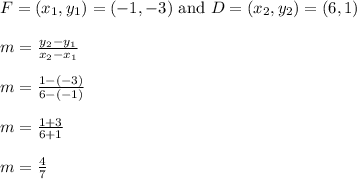
The slope of line FD is 4/7.
--------------------------
To recap everything so far, we found the following:
- slope of DE = -1/2
- slope of EF = 2
- slope of FD = 4/7
The product of the first two slopes gets us (-1/2)*(2) = -1 showing that DE is perpendicular to EF.
Perpendicular slopes multiply to -1 as long as neither line is vertical nor horizontal.
Since DE is perpendicular to EF, this proves we have a 90 degree angle at point E.
Therefore triangle DEF is a right triangle.