9514 1404 393
Answer:
(x -3)/(x -1) and (x +2)/(x -3)
Explanation:
If you want the product of two fractions to be a/b, then 'a' must be a factor in the numerator of one of them, and 'b' must be a factor in the denominator of one of them.
'a' and 'b' are already in the numerator and denominator of a/b, so we can choose the other fraction to be something that has a value of 1, such as c/c.
(a/b)(c/c) = (ac)/(bc) = a/b
The intermediate product (before we reduce the result) has a numerator of 'ac' and a denominator of 'bc'. We can split those into two parts however we like. For example, we can get the same result by multiplying ...
(a/c)(c/b) = (ac)/(bc) = a/b
So, a simple answer to your question could be ...
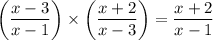
__
The idea is to multiply the given result by 1 in some form. That form can be as complicated as you like, and its factors can be grouped any way you like