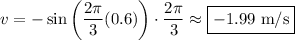Question

The displacement of an object in SHM is described by the equation


`x = cos\binom{2\pi}{3}t`
where x is in meters and t in seconds. Determine the velocity of the object at t = 0.6 s. ​

Answer 1

`-1.99\:\mathrm{m/s}`

Step-by-step explanation:

Assuming that the equation is intended to be
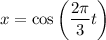`\displaystyle x=\cos\left((2\pi)/(3)t\right)`, we can find the velocity vs. time equation by taking the first derivative with respect to
`t`:

`\displaystyle (dx)/(dt)=(d)/(dt)\left(\cos\left((2\pi)/(3)t\right)\right)`

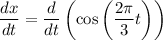
Recall the chain rule:

`\displaystyle f(g(x))'=f'(g(x))\cdot g'(x)`

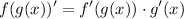
Therefore,

`\displaystyle (d)/(dt)\left(\cos\left((2\pi)/(3)t\right)\right)=-\sin\left((2\pi)/(3)t\right)\cdot (2\pi)/(3)`

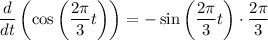
Therefore, the velocity vs. time equation of the object is
`\displaystyle v=-\sin\left((2\pi)/(3)t\right)\cdot (2\pi)/(3)`.

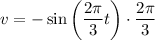Substitute
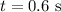`t=0.6\text{ s}` into this equation to find the velocity at that given time:

`\displaystyle v=-\sin\left((2\pi)/(3)(0.6)\right)\cdot (2\pi)/(3)\approx \boxed{-1.99\text{ m/s}}`