Answer:

This is the same as writing y = (1/3)x - 2
Slope = 1/3
y intercept = -2
======================================================
Step-by-step explanation:
We first need to determine the slope

Then we'll use this value of m, along with (x,y) = (15,3), to determine the y intercept b value.
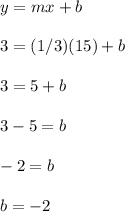
You could use the other point (-3,-3) as well

Either way, we end up with the same y intercept. You don't need to show both sets of steps when computing b. You only need to pick one set of steps.
Since m = 1/3 and b = -2, we go from y = mx+b to y = (1/3)x - 2 which is the same as writing
