Problem 2
- x = amount of candy Ian got
- y = amount of candy Joe got
- z = amount of candy Josh got
Based on those variables, we can form these equations
- x+y+z = 75 since all three got 75 total
- x = 3y+6 due to "Ian collected six more than three times the amount Joe got"
- z = y-11, since Josh collected 11 pieces less compared to Joe
The system of equations is
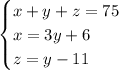
Let's start with the first equation. Then apply substitution like so
x+y+z = 75
3y+6+y+z = 75 ... plug in x = 3y+6
4y+6+z = 75
4y+6+y-11 = 75 ... plug in z = y-11
5y-5 = 75
5y = 75+5
5y = 80
y = 80/5
y = 16 = amount of candy Joe collected
z = y-11 = 16-11 = 5 = amount Josh collected
x = 3y+6 = 3*16+6 = 54 = amount Ian collected
Answer: 54 pieces of candy
======================================================
Problem 3
x = number of pounds of candy that sells for $1.49 a pound
1.49x = cost of buying those x pounds of candy at that unit price
4.50*5 = 22.50 = cost of buying 5 pounds at $4.50 per pound
1.49x+22.50 = total cost
x+5 = total weight in pounds
(total cost)/(total weight) = final cost per pound
(1.49x+22.50)/(x+5) = final cost per pound
(1.49x+22.50)/(x+5) = 3.64
1.49x+22.50 = 3.64(x+5)
1.49x+22.50 = 3.64x+18.20
22.50-18.20 = 3.64x-1.49x
4.30 = 2.15x
2.15x = 4.30
x = (4.30)/(2.15)
x = 2
Answer: 2 pounds
======================================================
Problem 5
g = number of ghosts
w = number of witches
s = number of scarecrows
g+w+s = 22 = total number of items
w = g+1 since there's one more witch compared to ghosts
s = w-7 since there's 7 less scarecrows than witches
The system we need to solve is
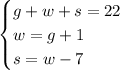
We'll use substitution here as well
g+w+s = 22
g+w+w-7 = 22 ... plug in s = w-7
g+2w-7 = 22
g+2(g+1)-7 = 22 ... plug in w = g+1
g+2g+2-7 = 22
3g-5 = 22
3g = 22+5
3g = 27
g = 27/3
g = 9, there are 9 ghosts
w = g+1 = 9+1 = 10 witches
s = w-7 = 10-7 = 3 scarecrows
Answers:
10 witches and 3 scarecrows