Answer:
x = 3.08 (3 s.f.)
Explanation:
Area of a Triangle (using sine)
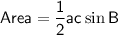
where:
- a and c are adjacent sides
- B is the included angle
Given:
- Area = 4√2 m²
- a = (2x - 3) m
- c = (x + 2) m
- B = 45°
Substitute the given values into the formula:
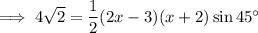
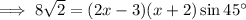
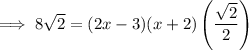
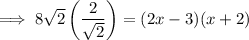
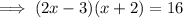
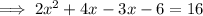
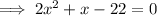
Use the Quadratic Formula to solve for x:
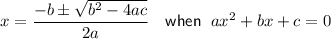
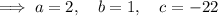
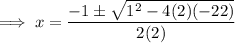

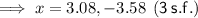
As distance is positive:
