Answer:
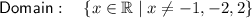
Explanation:
Given functions:
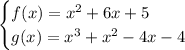
Factor function f(x):

Factor function g(x):
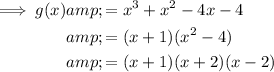
Therefore the composite function is:

A rational function is undefined when the denominator equals zero.
Therefore, the given composite function is undefined when (x+1)(x+2)(x-2)=0:
The domain of a function is the set of all possible input values (x-values).
Therefore, as the composite function is undefined when x = -1, x = -2 and x = 2, the domain is: