Question

1. What is the equation, in standard form, of a parabola that contains the following points? (1 point)

(-2, 18), (0.2). (4, 42)
Oy=-222 - 2x - 3
Oy=-3x2 + 2x - 2
Oy = 3x2 - 2x + 2
Oy=-2x2 + 3x + 2

Answer 1

y=3x2−2x+2

Explanation:

Standard form of equation of a parabola is
`y=ax^2+bx+c`

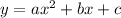
As it passes through points (−2,18), (0,2) and (4,42), each of these points satisfies the equation of parabola and hence

18=a⋅4+b⋅(−2)+c or 4a−2b+c=18 ........(A)

2=c ........(B)

and 42=a⋅16+b⋅4+c or 16a+4b+c=42 ........(C)

Now putting (B) in (A) and (C), we get

4a−2b=16 or 2a−b=8 and .........(1)

16a+4b=40 or 4a+b=10 .........(2)

Adding (1) and (2), we get 6a=18 or a=3

and hence b=2⋅3−8=−2

Hence equation of parabola is
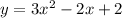`y=3x^2 -2x+2` and it appears as shown below

graph{3x^2-2x+2 [-10.21, 9.79, -1.28, 8.72]}