Answer:
y = –2(x – 1)² + 1
Explanation:
Given the quadratic function, y = -2x²+ 4x - 1:
where a = -2, b = 4, and c = -1
The vertex of a parabola is the point on the graph where the parabola intersects the axis of symmetry. The axis of symmetry occurs at x = h. Therefore, the x-coordinate of the vertex is the same as h.
To find the vertex, (h, k), you need to solve for h by using the formula:
Plug in the values into the formula:
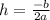
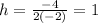
Therefore, h = 1.
Next, to find the k, plug in the value of h into the original equation:
k = -2x²+ 4x - 1
k = -2(1)²+ 4(1) - 1
k = 1
Therefore, the value of k = 1.
The vertex (h, k ) occurs at point (1, 1).
Now that you have the value for the vertex, you can plug these values into the vertex form:
y = a(x - h)² + k
a = determines whether the graph opens up or down; it also makes the parent function wider or narrower.
- If a is positive, the graph opens up.
- If a is negative, the graph opens down.
h = determines how far left or right the parent function is translated.
k = determines how far up or down the parent function is translated.
Plug in the vertex, (1, 1) into the vertex form:
y = –2(x – 1)² + 1
This parabola is downward facing, with its vertex, (1, 1) as its maximum point on the graph.