5. The length of line AB is equal to 14 units.
6. The length of line AB is equal to 2 units.
In Geometry, the corresponding side lengths are proportional to the lengths of corresponding sides when two triangles are similar.
Part 5.
Based on the side, angle, side (SSS) similarity postulate, we can logically deduce the following proportional side lengths;
AB/DE = BC/EF
7x/7 = 4/x
By cross-multiplying, we have;
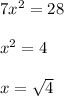
x = 2 units.
Now, we can find the length of line AB;
Length of line AB = 7x
Length of line AB = 7 × 2
Length of line AB = 14 units.
Part 6.
Based on the side, angle, side (SSS) similarity postulate, we can logically deduce the following proportional side lengths;
AC/DF = AB/DE
(x + 2)/(x + 6) = x/4
By cross-multiplying, we have;
4(x + 2) = x(x + 6)
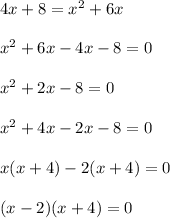
x = 2 or x = -4
Since a line segment cannot have a negative measurement, the length of AB is 2 units.