Question

A 26 ft ladder leaning against a wall begins to slide. How fast is the top of the ladder sliding down the wall at the instant of time when the bottom of the ladder is 10 ft from the wall and sliding away from the wall at the rate of 3 ft/sec?

Answer 1

The top of the ladder is sliding down at a rate of -1.25 ft/s.

Explanation:

From the Pythagorean Theorem:

`\displaystyle a^2 + b^2 = c^2`

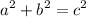
(Where a is the height, b is the distance between the bottom of the ladder and the wall, and c is the length of the ladder itself.)

Note that the hypotenuse c is a constant value at 26 feet. Substitute:

`\displaystyle a^2 + b^2 = (26\text{ ft})^2 = 676 \text{ ft}^2`

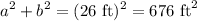
We want to determine how fast the top of the ladder is sliding down the wall at the instant of time when the bottom of the ladder is 10 feet from the wall and sliding away from the wall at the rate of 3 ft/s.

In other words, we want to find da/dt given that b = 10 ft, and db/dt = 3 ft/s.

First, we can differentiate both sides with respect to t, where a and b are both functions of t:

`\displaystyle (d)/(dt)\left[ a^2 + b^2\right ] = (d)/(dt)\left [ 676 \text{ feet}^2\right ]`

Implicit differentiation yields:

`\displaystyle 2a (da)/(dt) + 2b (db)/(dt) = 0`

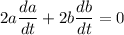
Next, since we know that b = 10 ft, we can find a:

`\displaystyle \begin{aligned} a^2 + b^2 & = 676\text{ ft}^2 \\ \\ a^2 +(10 \text{ ft})^2 & = 676\text{ ft}^2 \\ \\ a & = 24\text{ ft} \end{aligned}`

Substitute and solve for da/dt:

`\displaystyle \begin{aligned} 2a (da)/(dt) + 2b(db)/(dt) & = 0 \\ \\ 2(24 \text{ ft}) (da)/(dt) + 2(10 \text{ ft})(3 \text{ ft/s}) & = 0 \\ \\ 48 \text{ ft} \cdot (da)/(dt) & = -60 \text{ ft$^2$/s} \\ \\ (da)/(dt) & = -1.25 \text{ ft/s} \end{aligned}`

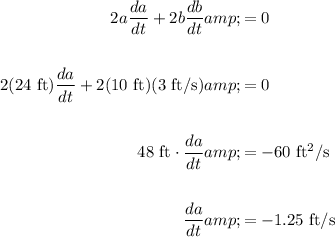
Since the ladder is sliding down the wall, da/dt is expected to be negative.

In conclusion, the top of the ladder is sliding down at a rate of -1.25 ft/s.