Answer:
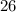 and
and
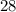 .
.
Explanation:
Let
 denote the smaller one of the two even integers (
denote the smaller one of the two even integers (
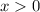 since both integers are positive.) The larger one of the two consecutive even integer would be
since both integers are positive.) The larger one of the two consecutive even integer would be
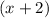 .
.
The square of the smaller integer would be
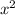 .
.
Five times the larger integer would be
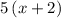 .
.
Subtract five times the larger integer from the square of the smaller integer to get
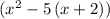 .
.
The value of this expression should be equal to
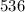 . In other words:
. In other words:
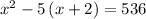 .
.
Rewrite and simplify this quadratic equation:
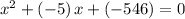 .
.
Apply the quadratic formula to find possible values of
 :
:
 .
.
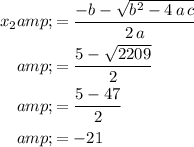 .
.
Since
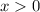 (both numbers are supposed to be positive),
(both numbers are supposed to be positive),
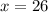 would be the only valid solution.
would be the only valid solution.
Therefore, the two integers would be
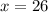 and
and
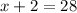 .
.