Answer:

Explanation:
Hi there!
First, find the slope of Line p:
 where two points that fall on the line are
where two points that fall on the line are
 and
and

Plug in the given points (5,−3) and (−2, 5):

Therefore, the slope of Line p is
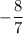 .
.
Perpendicular lines always have slopes that are negative reciprocals, such as 1/2 and -1/2, and 3/4 and -4/3.
Knowing this, the slope of a line perpendicular to Line p would be the negative reciprocal of
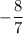 , which is
, which is
 .
.
I hope this helps!