Answer:
3, 8, 13, 18, 23
Explanation:
The nth term of an arithmetic sequence is
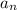 = a₁ + (n - 1)d
= a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Given a₄ = 18 and a₉ = 43 , then
a₁ + 3d = 18 → (1)
a₁ + 8d = 43 → (2)
Subtract (1) from (2) term by term, eliminating a₁
5d = 25 ( divide both sides by 5 )
d = 5
Substitute d = 5 into (1) for value of a₁
a₁ + 3(5) = 18
a₁ + 15 = 18 ( subtract 15 from both sides )
a₁ = 3 , then
a₂ = a₁ + 5 = 3 + 5 = 8
a₃ = a₂ + 5 = 8 + 5 = 13
a₄ = a₃ + 5 = 13 + 5 = 18
a₅ = a₄ + 5 = 18 + 5 = 23
The first 5 terms are 3, 8, 13, 18, 23