Answer:
The axis of symmetry is x = 1
The vertex of the parabola 2x² - 4x is (1, -2)
Explanation:
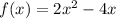
first find the axis of symmetry
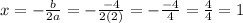
Now substitute this value back into the original equation and solve for f(x) = y
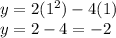
The vertex of the parabola is
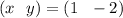
NOTE: separate the XY pair with a comma so
(x,y) = (1, -2)