Question

PLEASE HELP

A ball is thrown into the air from a height of 6 ft. The height, h, of the ball after t
seconds, is given by the equation h= -4.9+2 + 40t + 6. What is the maximum height
the ball reaches?
between 70 ft and 75 ft
between 75 ft and 80 ft
over 85 ft
between 80 ft and 85 ft

Answer 1

Over 85 ft

Explanation:

The maximum height of the ball is going to be located at the vertex of the parabola. First you need to find the x (or t in this case) coordinate for the axis of symmetry. Using the equation for the axis of symmetry of a parabola:

`x=(-b)/(2*a)`

`t=(-40)/(2*(-4.9))=(-40)/(-9.8)=4.0816`

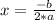
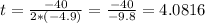
After finding the t-coordinate for the vertex, then plug this value into the original equation to find the corresponding h-coordinate:

Assuming the equation is
`h=-4.9t^(2)+40t+6`,

`h=-4.9(4.0816)^(2)+40(4.0816)+6=-81.6313+163.264+6=87.6327`

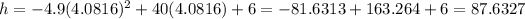
So the vertex can be represented as (4.016, 87.6327)

The maximum height is over 85 ft.