Question

The area of a rectangle gets reduced by 9 sq. units,if its length is reduced by 5 units and Breadth is increased by 3 units.If we increase the length by 3 units and Breadth 2 units ,the area increases by 67 units. Find the dimensions of rectangle. ​

Answer 1

Let the length and breadth of the rectangle be x and y.

Area of rectangle is A = xy

Therefore, the new length will be = x-5

Therefore, the new breadth will be = y + 3

So new area will be xy-9

Now the new relation will be (x+3)(y+2)=xy+67

.

Cross – multiplication method–

`</p><p></p><p>\frac{x}{{{b_1}{c_2} - {b_2}{c_1}}} =</p><p></p><p>\frac{y}{{{a_2}{c_1} - {c_2}{a_1}}} = \frac{1}{{{a_1}{b_2} - {a_2}{b_1}}} || x = \frac{{{b_1}{c_2} - {b_2}{c_1}}}{{{a_1} {b_2} - {a_2}{b_1}}} y = \frac{{{a_2}{c_1} - (c_2}{a_1}}}{{{a_1}{b_2}-{a_2}{b_1}}}\\`

`\Rightarrow \frac{x}{{305 - ( - 18)}} =\frac{y}{{ - 12 - ( - 183)}} = \frac{1}{{9 - 10)}}\\\`

`\Rightarrow \frac{x}{{323}} = \frac{y}{{171}} = \frac{1}{{19}} \\\Rightarrow x = 17, y = 9 \\`

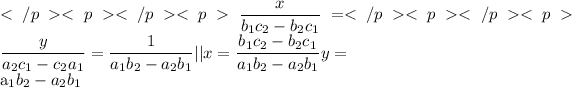
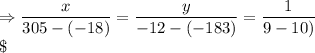
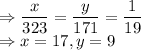
Therefore, the length is 17 and breadth is 9.