Answer:
Increasing
Explanation:
We are given the function:
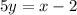
Since y is the function of x; we isolate y by dividing both sides by 5.
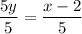
Thus:
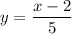
Simplify the expression, separating the fraction.
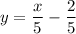
Familiar with this equation? This function is a linear function.
Now to the increasing and decreasing part. There are several ways to find whether if the graph is increasing.
- By substituting values
- Graph Visualization (Or look at the graph)
I will demonstrate the first method. Start from substituting negative to positive, if we keep substituting higher numbers and we get higher y-value then the graph is increasing.
If we substitute higher numbers but we get lower y-value then the graph is decreasing.
Substitution
y = -1/5 - 2/5 = -3/5
y = 0-2/5 = -2/5
y = 1/5-2/5 = -1/5
y = 2/5-2/5 = 0
y = 3/5-2/5 = 1/5
y = 4/5-2/5 = 2/5
y = 5/5-2/5 = 3/5
y = 6/5-2/5 = 4/5
...
As so on, as we see, when x keeps increasing, y increases too.
Therefore, the graph is increasing.