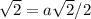Question

Given a square ABCD with side length equal to 'a'. From side AB, draw a line extending from point B in the opposite direction of point A, and place point B1 on the line continuing from side AB where AB1 = AC. Use the concatenated side BB1 to create a square BB1C1D1. Then, from side BB1, draw a line extending from point B1 in the opposite direction of point B, and place point B2 on the line connecting from this side BB1, where BB2 = BC1. Given point B1, B2, B3, ... As described above, find the sum of the lengths of the line segments AB, BB1, B1B2, ...

Please show your work too — thanks!
Topic: Infinite Geometric Series​

Answer 1

• 
  `a√(2)/2`

Explanation:

AB = a - given

BB₁ is the difference of the diagonal and side of the square with side a:

• BB₁ =
  `a√(2) -a=a(√(2)-1)`

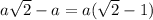
Each subsequent line segment is
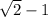`√(2)-1` times the previous.

So we have a GP with the first term of a and common ratio of
`√(2)-1`.

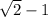The sum of the lengths is the sum of infinite GP:

• S = a/(r -1 ), where a - the first term and r - common ratio > 1

So the sum is:

• S = a/(
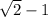  `√(2)-1` - 1) = a/
  `√(2) =a√(2)/2`