Given 'n' is a positive integer and 'r' is a real number which r > 1
Given the sequence {a_n} corresponding to:
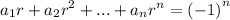
Answer the following questions:
( 1 )
Write a1,a2,a3 in term of r.
( 2 )
When n ≥ 2, write a_n in term of r.
( 3 )
Evaluate the sum of Infinite Series a1+a2+...+an+...
Thanks in advance!